Project B9 • Dynamical low-rank approximation for the simulation of radiation heat waves

Principal investigators

Project summary

Introduction

An interesting problem in the study of radiation phenomena is the penetration of radiation from a hot source into a cold material. As the material heats, a wave of thermal energy starts to propagate into it. Such propagating radiation fronts are called Marshak waves. Practical examples are the penetration of stellar radiation into the interstellar medium (star formation or supernova explosion), the radiation emitted from a hohlraum striking a fusion target, or laser wakefield acceleration through pressure waves [Mar58, Mih84, ZR67]. 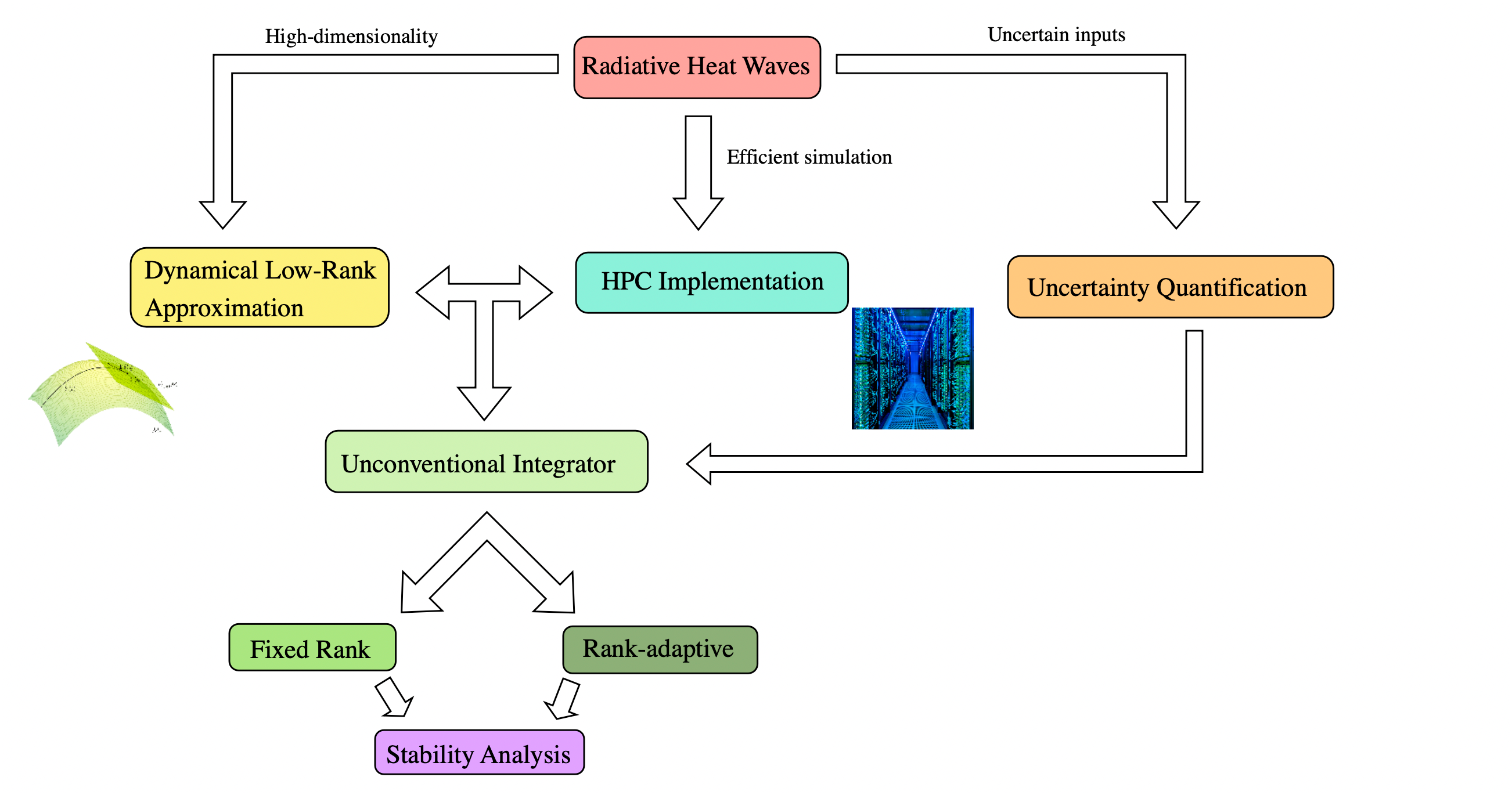All of these examples are of current interest in applications and are still challenging for high-performance computing (HPC) simulations.

We consider the thermal radiative transfer equations, which consist of the radiation transport equation plus a temperature equation for the medium [LPB83, MHB08] \begin{equation}\tag{1a}\label{eq:RadTransfer1} \frac{1}{c}\partial_{t}f + \Omega\cdot\nabla_{x}f = \sigma_{s}(\phi - f) + \sigma_{a}(B(T) - f), \end{equation} \begin{equation}\tag{1b}\label{eq:RadTransfer2} c_{\nu}\partial_{t}T = \int_{0}^{\infty}\int_{S^{2}}\sigma_{a}(f - B(T)) \mathrm{d}\Omega\mathrm{\nu}. \end{equation} For the sake of compactness of notation, all the independent variables have been suppressed. The unknowns in the above equation are the specific intensity of radiation $f(t,x,\Omega,\nu)$ at time $t$, position $x\in\mathbb{R}^{3}$, and frequency $\nu>0$, propagating in the direction $\Omega\in S^{2}$ and the temperature $T(t,x)$ of the background medium through which the radiation propagates. In the above equations $c$ denotes the speed of light and $c_\nu$ the material's heat capacity, which is assumed to be constant. The scattering cross section $\sigma_{s}(x,\nu,T(t,x))$ and absorption cross section $\sigma_{a}(x,\nu,T(t,x))$, which describe the material properties of the background medium, depend non-linearly on $T$ [Cha11]. The scalar flux is $\phi(t,x) =\int_{0}^{\infty} \int_{s^{2}}f(t,x,\Omega,\nu)\mathrm{d}\Omega\mathrm{\nu}$. In \eqref{eq:RadTransfer1}, the non-linear dependence $B(T)$ is kept Planckian, which also depends on the frequency.

Equation \eqref{eq:RadTransfer1} describes the dynamics of the photons that undergo isotropic scattering and can be absorbed by a background medium. This absorption of particles leads to an increase in the temperature of the background material according to \eqref{eq:RadTransfer2} which in turn emits blackbody radiation at its temperature. The coupling of the two equations is not only due to absorption but also due to the fact that the interaction cross sections of the medium depend on both, the frequency and the temperature. The phase space of the problem is high-dimensional (3 space, 2 angle, 1 frequency) and thus the problem is challenging to solve numerically. However, in relevant physical regimes there are indications that the actual dynamics take place close to a low-dimensional manifold, the Rosseland diffusion limit [LPB83].

Dynamical low-rank approximation (DLRA)

The dynamical low-rank approximation (DLRA), with its origins in quantum dynamics [Dir30, MGW09, MMC90], was mathematically analysed in a series of papers [KL07, KL10, Lub08, LRSV13]. Originally, it was proposed for matrix differential equations (MDEs) and then later extended to tensors [KL10, LRSV13]. The original method, as proposed in [KL07], is based on using an SVD-like ansatz for the low-rank solution of the given MDE, $\dot{Y}(t) = F(Y(t))$, where $Y(t),F(Y(t))\in\mathbb{R}^{m\times n}$. The right hand side of the MDE is then projected onto the tangent space ($\mathcal{T}_{Y}\mathcal{M}_{r}$) to the low-rank manifold ($\mathcal{M}_{r}$) at the current approximation ($Y$). The resulting evolution equations are then solved using standard solvers. While the idea seems rather simple, it has become a cornerstone in simulation of high-dimensional PDEs with low-rank solutions and sparked a greater interest in computational kinetic theory (CKT) [EL18, EL19, EJ21, DEL21].

A major breakthrough for the time integration of these reduced differential equations was achieved by decomposing the tangent space projection into three sub-projections and then applying a projector-splitting method [LO14]. This is known as the projector-splitting integrator (PSI) [LO14] in the literature. One of the key advantages for CKT is that using the method reduces both the computational effort as well as the memory footprint from $\mathcal{O}(mn)$ to $\mathcal{O}(mr + nr + r^{2})$.

"Unconventional" DLRA integrator (UI)

Read more. View less.

Rank-adaptivity for UI

Read more. View lessspan>

Stability of UI and PSI

Read more. View less.

The choice of PSI or UI to solve the evolution equations, arising from DLRA, becomes an important factor when considering stability in hyperbolic problems. While the UI yields smoother solution profiles for first-order moments (such as scalar flux in radiation transport), it heavily dampens higher-order moments [KCEF22]. In contrast, the PSI provides a more adequate representation of higher-order moments while producing oscillatory first-order moments [KCEF22]. Additionally, it is also not clear how to choose a CFL (Courant–Friedrichs–Lewy) condition for DLRA. In [KEC23] these questions are investigated and a new stability analysis for the non-linear DLRA equations is presented along with a stabilisation for PSI based on performing DLRA in continuous form.

Simulating Marshak waves

Simulating Marshak heat waves is a computationally expensive problem (see Introduction for explanation), thus to obtain a numerically efficient method [CFK22] propose using DLRA as a model reduction technique. This has been performed in conjuncture with a discontinuous Galerkin discretisation in space and spectral approximation in angle. The resulting simulations using PSI and UI agree very well with the reference solution (full method without DLRA) while requiring only 5.8% of the time required to compute the reference solution. In the following figures, the UI is referred to as "BUG" integrator standing for basis update & Galerkin integrator.

Dose calculation in radiation therapy

Radiation therapy is a medical procedure to treat cancer which uses high-energy particles to irradiate cancer cells and destroy them. The continuous slowing down (CSD) approximation [LMFB97] to the linear Boltzmann equation provides an accurate model for the transport of particles through the human body. This allows for the calculation of the dose of irradiated particles at the target site. The integrators developed in this project were used to resolve the dynamics of the collided particles in a collided and uncollided split of the linear Boltzmann equation, while an efficient full-rank solver was used for the uncollided particles [KS22].

Quantifying high-dimensional uncertainties

In a large amount of applications, that can be modelled by hyperbolic conservation laws (e.g. radiation transport), uncertainty is observed in its input parameters (e.g. initial-, boundary conditions, or modelling parameters). These uncertainties may arise as a result of modelling assumptions as well as measurement or discretisation errors and can heavily influence the behaviour of the system at hand. Uncertainty quantification for hyperbolic problems poses several challenges, such as spurious oscillations [MKNG04, Bar13, DWB13], the loss of hyperbolicity [PDL09], or the exponential growth of the number of unknowns when the dimension of the random domain increases. DLRA can be used to mitigate the high computational cost and memory footprint that may arise due to high-dimensional uncertainty and this has been done for uncertain Burger's equation in [KCEF22].

Publications

1. J. Kusch and P. Stammer. A robust collision source method for rank adaptive dynamical low-rank approximation in radiation therapy. ESAIM: Math. Model. Numer. Anal., 57(2):865–891, March 2023. URL https://doi.org/10.1051/m2an/2022090. [preprint] [files] [bibtex]

2. J. Kusch, L. Einkemmer, and G. Ceruti. On the stability of robust dynamical low-rank approximations for hyperbolic problems. SIAM J. Sci. Comput., 45(1):A1–A24, February 2023. URL https://doi.org/10.1137/21M1446289. [preprint] [files] [bibtex]

3. J. Kusch, B. Whewell, R. McClarren, and M. Frank. A low-rank power iteration scheme for neutron transport criticality problems. J. Comput. Phys., 470:111587, December 2022. URL https://doi.org/10.1016/j.jcp.2022.111587. [preprint] [files] [bibtex]

4. G. Ceruti, J. Kusch, and C. Lubich. A rank-adaptive robust integrator for dynamical low-rank approximation. BIT, 62(4):1149–1174, December 2022. URL https://doi.org/10.1007/s10543-021-00907-7. [preprint] [bibtex]

5. J. Kusch, G. Ceruti, L. Einkemmer, and M. Frank. Dynamical low-rank approximation for Burgers' equation with uncertainty. Int. J. Uncertain. Quantif., 12(5):1–21, March 2022. URL https://doi.org/10.1615/Int.J.UncertaintyQuantification.2022039345. [preprint] [files] [bibtex]

6. G. Ceruti and C. Lubich. An unconventional robust integrator for dynamical low-rank approximation. BIT, 62(1):23–44, March 2022. URL https://doi.org/10.1007/s10543-021-00873-0. [preprint] [bibtex]

7. G. Ceruti, C. Lubich, and H. Walach. Time integration of tree tensor networks. SIAM J. Numer. Anal., 59(1):289–313, February 2021. URL https://doi.org/10.1137/20M1321838. [preprint] [bibtex]

8. Z. Peng, R. G. McClarren, and M. Frank. A low-rank method for two-dimensional time-dependent radiation transport calculations. J. Comput. Phys., 421:109735, 18, November 2020. URL https://doi.org/10.1016/j.jcp.2020.109735. [bibtex]

9. G. Ceruti and C. Lubich. Time integration of symmetric and anti-symmetric low-rank matrices and Tucker tensors. BIT, 60(3):591–614, January 2020. URL https://doi.org/10.1007/s10543-019-00799-8. [preprint] [bibtex]

Preprints

10. C. Patwardhan, M. Frank, and J. Kusch. Asymptotic-preserving and energy stable dynamical low-rank approximation for thermal radiative transfer equations. CRC 1173 Preprint 2024/6, Karlsruhe Institute of Technology, February 2024. [files] [bibtex]

11. G. Ceruti, M. Frank, and J. Kusch. Dynamical low-rank approximation for Marshak waves. CRC 1173 Preprint 2022/76, Karlsruhe Institute of Technology, December 2022. [files] [bibtex]

Theses

12. G. Ceruti. Unconventional contributions to dynamical low-rank approximation of tree tensor networks. PhD thesis, University of Tübingen, July 2021. [bibtex]

13. J. Kusch. Realizability-preserving discretization strategies for hyperbolic and kinetic equations with uncertainty. PhD thesis, Karlsruhe Institute of Technology, May 2020. [bibtex]

Other references

14. L. Einkemmer and I. Joseph. A mass, momentum, and energy conservative dynamical low-rank scheme for the Vlasov equation. J. Comput. Phys., 443:Paper No. 110495, 16, 2021. URL https://doi.org/10.1016/j.jcp.2021.110495. [bibtex]

15. Z. Ding, L. Einkemmer, and Q. Li. Dynamical low-rank integrator for the linear Boltzmann equation: error analysis in the diffusion limit. SIAM J. Numer. Anal., 59(4):2254–2285, 2021. URL https://doi.org/10.1137/20M1380788. [bibtex]

16. L. Einkemmer and C. Lubich. A quasi-conservative dynamical low-rank algorithm for the Vlasov equation. SIAM J. Sci. Comput., 41(5):B1061–B1081, 2019. URL https://doi.org/10.1137/18M1218686. [bibtex]

17. L. Einkemmer and C. Lubich. A low-rank projector-splitting integrator for the Vlasov-Poisson equation. SIAM J. Sci. Comput., 40(5):B1330–B1360, 2018. URL https://doi.org/10.1137/18M116383X. [bibtex]

18. C. Lubich and I. V. Oseledets. A projector-splitting integrator for dynamical low-rank approximation. BIT, 54(1):171–188, 2014. URL https://doi.org/10.1007/s10543-013-0454-0. [bibtex]

19. T. Barth. Non-intrusive uncertainty propagation with error bounds for conservation laws containing discontinuities. In Uncertainty quantification in computational fluid dynamics, volume 92 of Lect. Notes Comput. Sci. Eng., pages 1–57. Springer, Heidelberg, 2013. [bibtex]

20. R. P. Dwight, J. A. S. Witteveen, and H. Bijl. Adaptive uncertainty quantification for computational fluid dynamics. In Uncertainty quantification in computational fluid dynamics, volume 92 of Lect. Notes Comput. Sci. Eng., pages 151–191. Springer, Heidelberg, 2013. [bibtex]

21. C. Lubich, T. Rohwedder, R. Schneider, and B. Vandereycken. Dynamical approximation by hierarchical Tucker and tensor-train tensors. SIAM J. Matrix Anal. Appl., 34(2):470–494, 2013. URL https://doi.org/10.1137/120885723. [bibtex]

22. M. Chadwick, M. Herman, P. Obložinský, M. Dunn, Y. Danon, A. Kahler, D. Smith, B. Pritychenko, G. Arbanas, R. Arcilla, R. Brewer, D. Brown, R. Capote, A. Carlson, Y. Cho, H. Derrien, K. Guber, G. Hale, S. Hoblit, S. Holloway, T. Johnson, T. Kawano, B. Kiedrowski, H. Kim, S. Kunieda, N. Larson, L. Leal, J. Lestone, R. Little, E. McCutchan, R. MacFarlane, M. MacInnes, C. Mattoon, R. McKnight, S. Mughabghab, G. Nobre, G. Palmiotti, A. Palumbo, M. Pigni, V. Pronyaev, R. Sayer, A. Sonzogni, N. Summers, P. Talou, I. Thompson, A. Trkov, R. Vogt, S. v. d. Marck, A. Wallner, M. White, D. Wiarda, and P. Young. ENDF/B-VII.1 Nuclear Data for Science and Technology: Cross Sections, Covariances, Fission Product Yields and Decay Data. Nuclear Data Sheets, 112(12):2887–2996, 2011. URL https://doi.org/10.1016/j.nds.2011.11.002. Special Issue on ENDF/B-VII.1 Library. [bibtex]

23. O. Koch and C. Lubich. Dynamical tensor approximation. SIAM J. Matrix Anal. Appl., 31(5):2360–2375, 2010. URL https://doi.org/10.1137/09076578X. [bibtex]

24. H.-D. Meyer, F. Gatti, and G. Worth. Multidimensional Quantum Dynamics. John Wiley & Sons, 2009. [bibtex]

25. G. Poëtte, B. Després, and D. Lucor. Uncertainty quantification for systems of conservation laws. J. Comput. Phys., 228(7):2443–2467, 2009. URL https://doi.org/10.1016/j.jcp.2008.12.018. [bibtex]

26. R. G. McClarren, J. P. Holloway, and T. A. Brunner. On solutions to the $P_n$ equations for thermal radiative transfer. J. Comput. Phys., 227(5):2864–2885, 2008. URL https://doi.org/10.1016/j.jcp.2007.11.027. [bibtex]

27. C. Lubich. From Quantum to Classical Molecular Dynamics: Reduced Models and Numerical Analysis. Zurich Lectures in Advanced Mathematics. European Mathematical Society (EMS), Zürich, 2008. [bibtex]

28. O. Koch and C. Lubich. Dynamical low-rank approximation. SIAM J. Matrix Anal. Appl., 29(2):434–454, 2007. URL https://doi.org/10.1137/050639703. [bibtex]

29. O. P. Le Maître, O. M. Knio, H. N. Najm, and R. G. Ghanem. Uncertainty propagation using Wiener-Haar expansions. J. Comput. Phys., 197(1):28–57, 2004. URL https://doi.org/10.1016/j.jcp.2003.11.033. [bibtex]

30. E. W. Larsen, M. M. Miften, B. A. Fraass, and I. A. Bruinvis. Electron done calculations using Method of Moments. Med Phys., 24(1):111–125, 1997. URL https://doi.org/10.1118/1.597920. [bibtex]

31. H.-D. Meyer, U. Manthe, and L. Cederbaum. The multi-configurational time-dependent Hartree approach. Chemical Physics Letters, 165(1):73–78, 1990. URL https://doi.org/10.1016/0009-2614(90)87014-I. [bibtex]

32. D. Mihalas and B. W. Mihalas. Foundations of Radiation Hydrodynamics. Oxford University Press, New York, 1984. [bibtex]

33. E. Larsen, G. Pomraning, and V. Badham. Asymptotic analysis of radiative transfer problems. J. Quant. Spectrosc. Radiat. Transfer, 29(4):285–310, 1983. URL https://doi.org/10.1016/0022-4073(83)90048-1. [bibtex]

34. Y. Zeldovich and Y. P. Raizer. Physics of Shock Waves and High Temperature Hydrodynamic Phenomen. Academic Press, 1967. [bibtex]

35. R. E. Marshak. Effect of radiation on shock wave behavior. Phys. Fluids, 1:24–29, 1958. URL https://doi.org/10.1063/1.1724332. [bibtex]

36. P. A. M. Dirac. Note on Exchange Phenomena in the Thomas Atom. Mathematical Proceedings of the Cambridge Philosophical Society, 26(3):376–385, 1930. URL https://doi.org/10.1017/S0305004100016108. [bibtex]