Associated Project AP9 • Quantized vortices and nonlinear waves

The project aims to explore dispersive effects in fluid flow with a focus on quantum fluids and (quantized) vortices. The purpose is two-fold: exploiting dispersive effects relevant for regularity and stability properties and second analyzing the dynamics of quantized vortices finalized to an understanding of quantum turbulence.
A quantum fluid is a system of interacting particles that exhibits effects of quantum statistics also at a macroscopic scale. Superfluid helium discovered in 1937 by Allen, Misener and Kapitza (Nobel prize 1978) constitutes its first experimental occurrence. In 1995, Bose-Einstein condensates (BEC), have first experimentally been realized in 1995 (Nobel prize 2001 for Cornell, Wiemann and Ketterle). Related models are relevant in engineering applications such as for the electron transport in semiconductor devices.

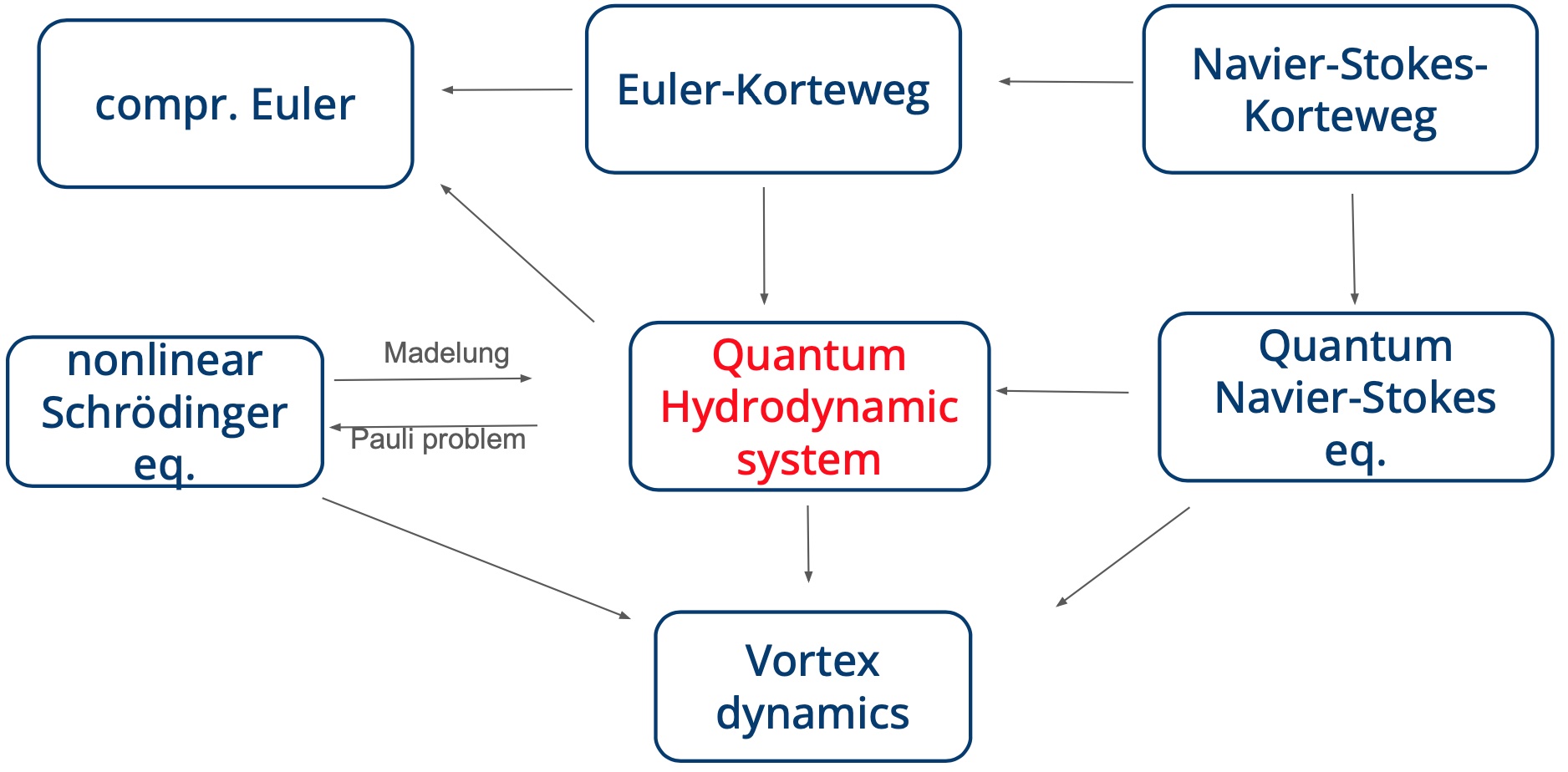
Mathematical Analysis. The prototype model is the so called Quantum Hydrodynamic system (QHD) describing an inviscid compressible fluid flow featuring a quantum correction term. From a mathematical perspective, the QHD system reads as a compressible Euler system augmented by a dispersive stress tensor. Its mathematical theory faces similar outstanding questions and difficulties as the well-known ones for the compressible Euler equations.
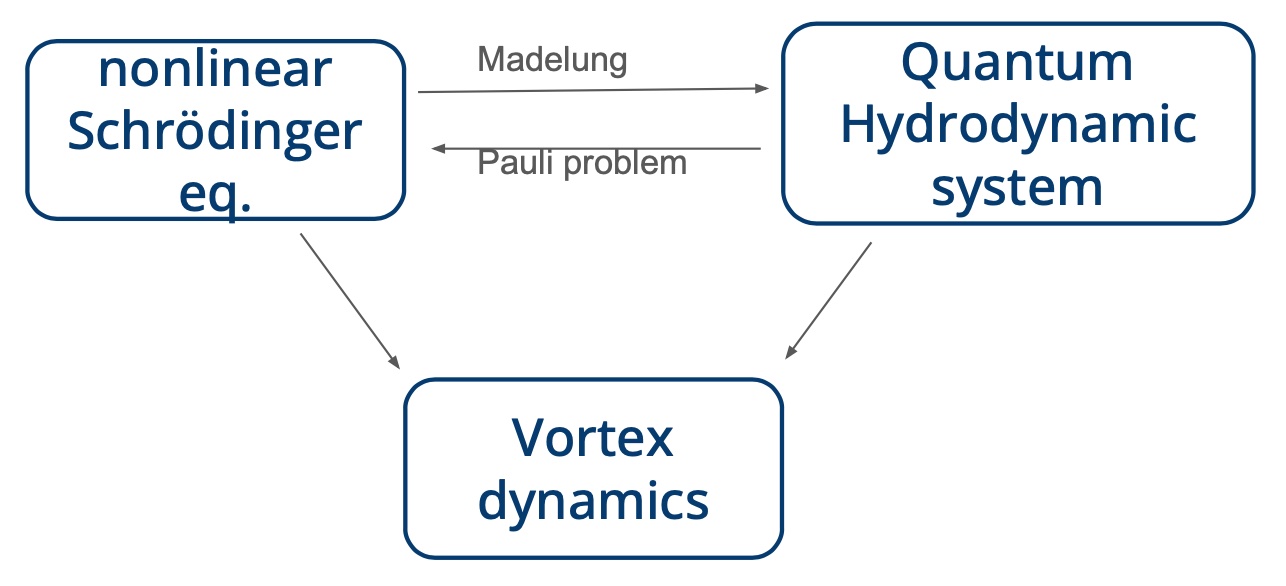
The QHD system admits a formal analogy to an effective wave-function dynamics through the Madelung transform. For BEC and superfluid helium, this Schrödinger type dynamics is provided by the Gross-Pitaevskii theory.
This motivates our hybrid approach combining both dispersive and hydrodynamic techniques to investigate fundamental physical phenomena. In the presence of vacuum, we rigorously justify the Madelung transform by a polar factorization method.

The project. A key theme is to elucidate peculiarities of the behavior of quantum fluid flow compared to classical hydrodynamics. Mathematically, this mainly translates to exploiting dispersive properties captured by Strichartz estimates in establishing a solution theory and the study of quantized vortices.
A robust understanding of the properties of quantized vortices is instrumental for a theory of (quantum) turbulence.
Non-trivial boundary conditions at spatial infinity provide the suitable framework to investigate physically relevant coherent structures. We are thus led to investigate

• nonlinear Schrödinger equations with non-vanishing conditions at infinity such as Gross-Pitaevskii equations. These equations admit a very rich dynamics in terms of particular solutions. The analysis of these equations is of independent interest and requires a suitable functional framework different from the usual $L^p$-based function spaces,
• hydrodynamic systems such as QHD, quantum Navier-Stokes eq. and related models with non-trivial far-field.

The hydrodynamic models describe evolution equations for the physical observables mass and current density. They allow for dissipative or viscous phenomena to be included in a natural way.
These models fall within the class of Korteweg or capillarity fluids to which our analysis extends. For general Korteweg fluids, an analogy to semi-linear NLS is no longer available.

Key questions and objectives. We address well-posedness at low regularity, singularity formation, quantitative and qualitative properties of solutions, singular limits and characterize relevant asymptotic dynamics, e.g. dynamics and interaction of vortices.